… and Using Your Noggin —
In my columns for the past 3 months, we have been discussing fault locating in the copper infrastructure with a multifunction test set. Based upon these columns, I’ve received several questions about using specific test set functions. In this month’s column, I address several of the most frequently asked questions, including:
• How does the test set convert ohms to feet or meters?
• How does temperature affect measurements?
• How does the test set account for gauge or temperature changes?
Converting Ohms to Feet or Meters
When converting linear wire resistance from ohms to feet or meters, how do I determine the gauge and/or the temperature of the cable pair, and what do I do if the gauge or temperature changes? Finding the gauge of a copper conductor by removing the insulation and looking at the bare copper conductor can fool you. Most vendors send a wire gauge with the test set. If yours is missing, contact your test set vendor. They will be happy to send you one.
InvisiLight® Solution for Deploying Fiber
April 2, 2022Go to Market Faster. Speed up Network Deployment
April 2, 2022Episode 10: Fiber Optic Closure Specs Explained…
April 1, 2022Food for Thought from Our 2022 ICT Visionaries
April 1, 2022First, for the field technician that is new to copper troubleshooting, a description of linear wire resistance. The linear wire resistance for the 4 basic conductors is given below.
• A 26-gauge copper conductor that is at a temperature of 68 degrees Fahrenheit has a linear wire resistance of 24 feet per ohm.
• A 24-gauge copper conductor that is at a temperature of 68 degrees Fahrenheit has a linear wire resistance of 38.54 feet per ohm.
• A 22-gauge copper conductor that is at a temperature of 68 degrees Fahrenheit has a linear wire resistance of 61.75 feet per ohm.
• A 19-gauge copper conductor that is at a temperature of 68 degrees Fahrenheit has a linear wire resistance of 124.24 feet per ohm.
That said, if I were to use a multifunction test set to measure the distance to a resistive fault such as a short, tip or ring ground, or crossed battery on a cable pair, and the distance to fault measured 10 ohms in 26-gauge wire at 68 degrees, I would expect to find the fault at 240 feet from where I took the measurement. In 24-gauge the fault would be 38.54 feet down the cable. As the diameter of the wire increases the resistance decreases and the distance to the fault increases. Additionally, as the temperature of the conductor increases, the resistance increases and the fee per ohm decreases.
Any change in resistance along the conductor route will affect bridge measurement distance. Such resistance changes are caused by gauge and gauge change or temperature and temperature change or both. When you enter the gauge and temperature into the RFL function of your multifunction test set the test set does it for you. Also, some test sets compute both gauge changes and temperature changes.
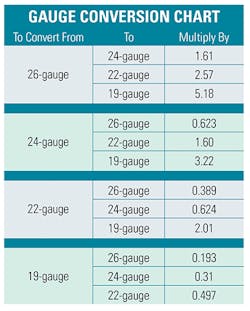
GAUGE CONVERSIONS
When a test set, using the RFL function, is testing through a gauge change the restive difference between the two gauges must be accounted for to determine physical distance to the fault. The following chart is used to convert from one gauge to another.
Following are examples of gauge and temperature conversions using the gauge conversion chart and the temperature formula.
SINGLE GAUGE CHANGE
With the RFL function set 24-gauge at 75 degrees distant to fault (DTF) shows 300 feet. The cable map indicates that 200 feet is 24-gauge and the rest of the cable is 22-gauge at 75 degrees.
Measurement: 300 ft. of 24 ga. at 75 degrees
Subtract: -200 ft. of 24 ga. at 75 degrees
Leaving: 100 ft. of 24 ga. at 75 degrees to be converted to 22 ga. at 75 degrees.
To convert 100 feet of 24-gauge measurement to 22-gauge multiply by 1.6 which indicates 160 feet of 22-gauge cable added to the 24-gauge gives an actual footage of 360 feet.
To locate the fault, add the 200 feet of 24 gauge to the 160 feet of 22 gauge.
The fault is 360 physical feet from the strap.
TEMPERATURE CHANGE
A resistive fault shows in an aerial cable in the sun with an outside temperature of 90 degrees. Measurements are taken at 130 degrees to account for the internal conductor temperature. Distance-to-fault measures 1,500 feet of 24 gauge at 130 degrees. The map indicates only 1,000 feet of cable at 130 degrees. The cable then goes buried back to a manhole 3,000 feet away. The buried temperature is 70 degrees. In order to calculate the distance from where the cable goes buried, use the following technique. Each degree of temperature change will affect the measurement by .00218 feet for each foot of cable.
Measurement: 1,500 ft. of 24 ga. at 130 degrees
Subtract: -1,000 ft. of 24 ga. at 130 degrees
Leaving: 500 ft. of 24 ga. at 130 degrees to be converted to 70 degrees. 130 degrees minus 70 degrees equals 60 degrees of temperature change.
Using the Formula:
Temperature change X ft/degree = change/ft
60 degrees X .00218= .1308
Multiply the change/foot by the section footage:
.1308 x 500 feet = 65.4 feet difference.
When the temperature change decreases, the difference must be added.
500 feet + 65.4 feet = 565.4 feet difference.
The fault is 565.4 feet into the buried section, or 1,565.4 feet from the test set.
Why learn gauge conversion? Simply put: to potentially save a lot of time by using your brain and an old-fashioned calculator. Here’s why: While test sets are amazing and automate much of your work, it does take time to make programming changes. When it’s 15 degrees or colder in Minnesota, do you want to hang around for 45 minutes to reprogram your set due to unanticipated changes such as temperature or gauge?
Like this Article?
Subscribe to ISE magazine and start receiving your FREE monthly copy today!
Signing off
Thank you, as always, for being such loyal readers and also for calling me when you believe I’ve made a mistake. I also really enjoy getting your calls for help. I’m retired but really miss being in the field. And my wife really likes it when I’m busy and can’t watch golf on TV. Reach out to me via email [email protected] or 831.818.3930.